Bending a Soccer Ball -- Mathematically 6 Animations of Morphings

June 2006

Quicktime Movie Downloads

A few weeks ago, Dana Mackenzie contacted me and asked if I could create some graphics for an article in American Scientist "The Topology and Combinatorics of Soccer Balls", by Dieter Kotschick, that Dana was editing at this time. Using various code pieces from the GuideBooks about tori, polyhedra, knots, Riemann surfaces, and the Weierstrass elliptic function (especially Graphics: 2.1.5, 2.3.2, 2.3.4, 2.3.7, Solution 2.2, 2.18, Numerics: 1.12.2, Symbolics: Solution 1.23, 3.9, 3.3, 3.4), I created the graphics shown in the article. As steps towards the graphics, the following animations were created.

See also: the "Soccer to soccer" movie that shows the construction of a triple cover of a Riemann sphere. (On Google Animations)

Smooth morphing a torus into double-covered soccer ball

The animation (3.8 MB, Quicktime .mov) shows how a torus is continuously deformed into two concentric soccer balls of identical size and orientation. No tearing of the surface occurs in this transition. The typically black pentagons of a soccer ball are colored differently for easy visual tracking of the morphing. The two final, staggered soccer balls are connected at four points at vertices of four of the twelve black pentagons.

More technically, the animation shows a smooth homotopy between the identity map and the map f(z), where

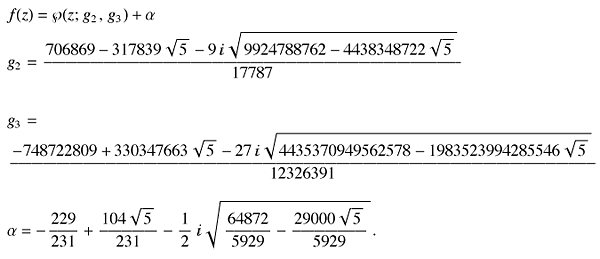
f(z) = P(z ; g_2, g_3) + α g_2 = (706869 - 317839 5^(1/2) - 9  (9924788762 - 4438348722 5^(1/2))^(1/2))/17787; g_3 = (-748722809 + 330347663 5^(1/2) - 27  (4435370949562578 - 1983523994285546
5^(1/2))^(1/2))/12326391;α = -229/231 + (104 5^(1/2))/231 - 1/2  (64872/5929 - (29000 5^(1/2))/5929)^(1/2) .

Here (z;, g₂, g₃) is the Weierstrass's elliptic function . The function is a doubly-periodic function and its natural domain is a period parallelogram in the complex z-plane. The period parallelogram is canonically mapped to a torus embedded in .

The map f(z) maps a period parallelogram to the whole complex plane twice. The complex plane is visualized through its Riemann sphere with a soccer tiling. The parameters g₂ and g₃ are complicated algebraic numbers and are chosen to make four vertices of the soccer ball branch points of the inverse map. The soccer ball tiling is oriented such that one vertex is the north pole, and one vertex of the pentagon that touches the North pole is on the Eastmost meridian.

Morphing a slit soccer ball into a torus

The animation (4.9MB, Quicktime .mov) shows how to transform a soccer ball with slits along two of its edges into a torus. Any two edges of equal type can be chosen. The two edges used were chosen to obtain a not-too-large stretching/compression of the pentagons/hexagons on the resulting torus. The morphing is based on a homotopy between a sphere and the stretched projection of the sphere onto a tube along a quarter circle (in toroidal coordinates) connecting the centers of the two slits. The tube is glued together at its two end (originally the two slits on the soccer ball surface) to form a torus.

Smooth morphing of a trefoil knot into a double-covered soccer ball

The animation (6.8MB, Quicktime .mov) shows a smooth homotopy between the identity map and the map f(z) from above. Three copies of the tiling from animation 1 are periodically repeated along the trefoil knot and then simultaneously mapped onto the Riemann sphere representing the soccer ball. This means that in the final graphics three pairs of soccer balls are coinciding.

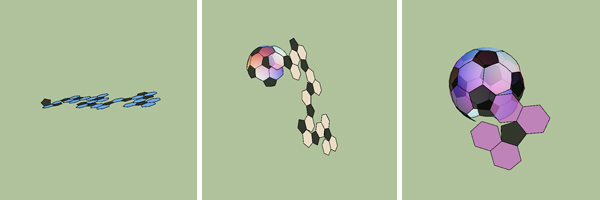
Folding a soccer ball from paper

The animation (3.1MB, Quicktime .mov) shows how to fold a soccer ball from a piece of paper. The (final) soccer ball is held fixed in space and the flat net of pentagons and hexagons is wound around it.

A 'breathing' soccer ball

The animation (2.9MB, Quicktime .mov) shows how the faces of a truncated icosahedron behave when the map →/ ${Overscript[r, →]}^α$ is applied to its faces. Depending on the sign of α, the faces either bulge in or out. For α=1, the round soccerball is recovered.

Moving a trefoil knot surface into hexa soccer ball

The animation (5.3MB, Quicktime .mov) shows another possibility to create a soccer ball from a trefoil knot with appropriate tiling. The elements of the tiling on the trefoil knot are first moved radially away from the knot and are then moved (and simultaneously shrunk) towards their position on the soccer ball according to the above map f(z).

Images calculated by Michael Trott, animated by Amy Young.